Each ethereum client and account identifies itself using a public key. The address is the last 20 bytes of the public key, usually displayed in hex format (0xf10ddd782c073D5644353a125F846E6Fc78ea235). Each public key is 64 bytes long and is created from a private key, which is kept secret. So how can we create a private and public key and how do they work?
Private key
The private key is 32 bytes long and is usually created completely random. This means that the private key is generated by the computer and then remembered by the user, instead of chosen by the user. That improves the security over passwords, because passwords are more easily guessable.
An example private key looks like this:
180236f4f6a7283fba078bed67fb14ebc8b7dcaecb1984ae8e6777b52ec31e6f
Users are really bad at remembering a string of characters looking like that. To help users remember, wallets often use a seed phrase:
oblige learn turkey front gift maid age unusual dutch creek puzzle caution
This string of random words can be transformed back into the bytes and the other way around.
Public key
The public key is created from the private key and is not secret. The generation will always generate the same public key from a private key.
So how do we do this? Well that turns out to involve a lot of super complicated math. The theory underlying this is called Elliptic curve cryptography (ECC). An example elliptic curve looks like this:
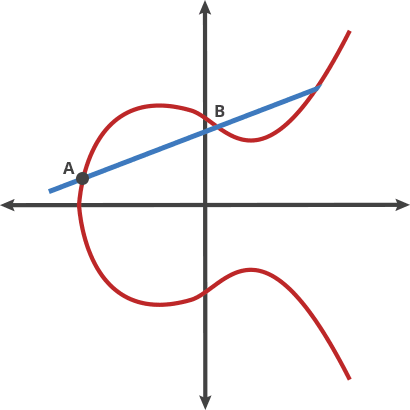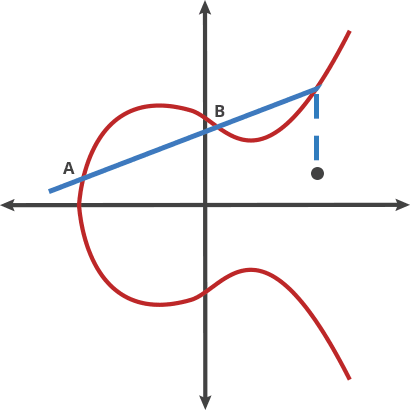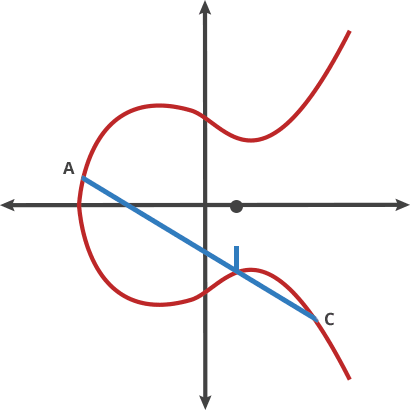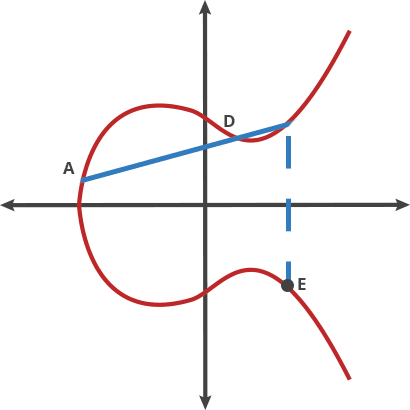
If we have a point on this curve, we can do A + A = B.
If we then add A and B and inverse that, we get point C.
We can then do A + C = D, and so on.
If we repeat this a lot of times (the private key is the amount), the resulting number is the public key.
This operation is called elliptic curve multiplication, and can be simplified as A * private = public.
This operation is irreversible, which means that looking at the public key, it’s impossible to find out what the private key was without brute forcing it (which takes way too long).
Point A is called the generator point and is set to a specific number according to the secp256k1 standard used by Bitcoin and Ethereum. This standard defines some parameters chosen in order to create a secure and efficient curve.
The curve shown above works with decimal numbers, but that is really hard too handle for a computer. That is why the actual curve only takes the whole numbers and wraps the numbers back to zero when they get to big (modulus operation):

This ends up looking a bit weird, but behaves exactly the same, with the added benefit that it’s now much easier to work with for a computer.
The private key used above is this decimal number:
10859421358633251808093415333513726222175123088472464898242245399478179929711
You might ask yourself how we can efficiently do A + B that amount of times. We can simplify the calculation a lot like this:
A + A + A + A = (A + A) + (A + A) = 2A + 2A
So when calculating A * N for a very large N, you only need to calculate A + 2A + 4A + 8A...
In the worst case, you need to calculate 256 terms.
Signing
So why is this useful? Because we can use it to sign messages, and proof that the messages come from us. This is how transactions work on Ethereum, when you send an instruction to swap on Uniswap, Metamask asks you to sign the transaction. By signing, you use your private key to create a signature that can be checked against your public key. Thus proving you gave permission to do the swap, without ever showing your private key.